아래 책을 보고있는데, 팡요랩이라는 곳에서 저자의 강의도 함께 있길레 들으면서 정리해본다.
바닥부터 배우는 강화 학습
강화 학습 기초 이론부터 블레이드 & 소울 비무 AI 적용까지이 책은 강화 학습을 모르는 초보자도 쉽게 이해할 수 있도록 도와주는 입문서입니다. 현업의 강화 학습 전문가가 직접 설명해 강화
book.naver.com
강화학습 기초 이론 - 인프런
강화학습의 이론, 기초 개념을 탄탄히 다지고 싶은 분, 딥러닝이 강화학습에 어떻게 적용 되는지 배우고 싶으신 분께 도움이 됩니다. 중급이상 인공지능 데이터 사이언스 강화학습 데이터 과학
www.inflearn.com
팡요랩의 강의는 DeepMind의 데이비드 실버의 강의를 좀 더 쉽게 전달하고자 만들어진 강의이다. 그래서 강의자료가 영어로 되어있고, 저도 한글화가 잘 안되는 부분은 영어로 작성할 것입니다. 아래에서 내가 캡쳐해서 쓰는 이미지는 모두 팡요랩의 강의자료에서 따왔다.
[Markov Decision Process]
이하 MDP

[1. Markov Processes]
[Introduction to MDPs]
MDP란? 강화 학습에서 환경을 설명하는 것. 여기서 환경은 완전히 관측 가능해야한다.
현재 state가 프로세스를 완전히 표현하는 것이 마르코프 property.
한마디로 강화학습을 formalize하는 것이다.
[Markov Property]

St에서 St+1로 갈 확률이 S1+ ... + St에서 St+1로 갈 확률과 같다.
이전 상황을 모두 버리고 직전 상황만으로도 다음 state로 갈 확률을 정할 수 있다. 이전 과거를 다 버릴 수 있다.
state가 모든 역사 정보를 가지고 있어서 history를 버릴 수 있다.
state는 미래에 대한 충분한 표현이다.

마르코프 프로세스에서는 action없이 매 step마다 정해진 확률로 다음 state로 옮겨다닌다. St에 있을때 다음 state가 여러개 있기에 Matrix로 표현된다.
위 Pss'은 State Transition Probability, 아래 matrix는 State Transition Matrix라고 한다.
Matrix의 각각의 row(행)의 합은 1이다.

memoryless : 이전까지 어느 경로를 통해서 왔던지 간에
random process : 샘플링을 할 수있다. 무슨 말이냐면 S1 - Sn까지 가는데 중간 state sequence들은 여러가지가 나올 수 있다. 정도로 받아 들이면 될듯.
S = state들의 집합.
P = 각 state들의 전이 확률 행렬.

Student MDP예제. ( 강의 한시간 지나서 얘기해주더라.. )
episode : start state에서 종료 state(여기선 Sleep)에 도달하면 episode라고 한다.
각 ㅁ(네모)들은 sampling된 것들.
그래서 위의 state process들의 probability를 matrix로 표현하면 아래와 같다.

[2. Markov Reward Process]
Reward가 있고 Maximize하는 것이다.

추가된 것. R, 감마.
어떤 state에 도달하면 reward를 줘라 라고 state마다 정의.

Edge에 reward를 줄 수 있을까?
- Markov process에는 action이라는게 없기때문에 'edge'를 선택할 수 없고 state만이 정의되어 있다.
- 뒤에 MDP에서는 state와 action에 reward가 주어진다. 다른 수업을 들으면 알 수있다.

Return
- 흔히 Reward를 Maximize하는게 아닌가 하지만 Reward와 Return은 다른 개념이다.
- Return이 더 정확한 표현. Reward를 그냥 받는 것이 아니라 Reward를 Discount 해서 Return받는다.
이를 maximize해야한다.
- 감마가 0에 가까울수록 "myopic" evaluation(근시안적인 평가) 그러니까, 순간적인 Reward가 중요
- 감마가 1에 가까울수록 "far-sighted" evaluation(원시안적인 평가) 장기적인 Reward가 중요.
accumulated discounted Reward를 Maximize하는게 목적이고 이 값을 Return이라고 한다.
꼭 discount를 해야할까 ? 왜 discount를 하는걸까 ?
1.수학적으로 편리해서. 이 discount때문에 수렴성이 증명이 된다.
수렴해야 크고 낮고를 평가할 수 있음.
2. 만약에 모든 sequence가 terminate 되는게 보장된다면 에피소드의 샘플링이 보장되니 감마를 1로 둘수도 있음.
문제 따라서 discount가 필요할 수도 있고, 덜 필요할수도 있음.

Value Function - State s에 도착했을때 Return의 기댓값
MDP일때 조금 달라진다. Gt는 확률변수다. 에피소드마다 Gt에 의해 샘플들이 나오는데 그들의 평균이다.

각 episode별 Expected return값을 평균내면 된다. 이렇게 평균을 내게 되면 C1 State에 도착했을 때 어느정도의 Return을 받을 것이라고 예측할 수 있음.



그래서 저 state들의 return 기댓값은 어떻게 구한다 ?
에피소드들을 샘플링해서 평균을 낸 값이다.
Bellman Euation for MRPs(너무너무 중요)
이걸 샘플링 안하고 어떻게 구할까.

S에서의 value는 한스탭을 가면 R(t+1)을 받는데 이것과 다음 state에서의 value의 감마 곱한것과 같다.
점화식으로 풀어둔것에 지나지 않음.

예를들어 s state에서 A와 B로 갈 수 있는데, v(s)= [s state에서의 return값]+ [A로 갔을때 return값 *A로 갈 확률] + [B로 갔을때 return값 * B로 갈 확률] . 갈수 있는 state가 A,B뿐만아니라 여러개 일 수 있으므로 시그마를 취했을 뿐이다.

값을 확인해보면 빨간원에서 원래 return값은 -2이고 0.4의 확률로 0.8에 갈수도 있고 0.6의 확률로 10에 갈수도 있다.
그러므로 v(s)= 4.3 = -2 + 0.4*0.8 + 0.6 * 10
MRP에서는 한번에 이렇게 풀 수 있는데, MDP에서는 한번에 안되서 iterative하게 풀어야한다.

v coumn vector인 행렬로 표현이 가능하다.

v로 묶고 역행렬을 양변에 곱하면 위의 식이 된다.
이식의 의미는 R, P , 감마가 주어져있으면 바로 풀 수 있다는 것이다. 왜냐하면 Bellman equation은 linear equation이기 때문이다.
알고리즘 복잡도가 O(n^3)이기 때문에 작은 문제(small state)에서만 연산이 가능하다.
선형대수학을 좀 배워야하는걸까.. 나 안배워봤는데..
[3. Markov Decision Process]
Markov process + (Reward , gamma) = Markov Reward Process
Markov Reward Process + Action = Markov Decision Process


State의 Reward가 사라지고 Action에 Reward가 적용됐다. Action을 하면 State가 변하는게 아니라 Action을 하면 확률적으로 State가 변한다...? 아래 검은 점(Pub)을 보면 0.2, 0.4, 0.4 확률값이 있듯 Action을 결정하고 그 Action에 맵핑된 확률로만 Action이 실행된다.(Action이 실행되야 State가 변한다)

MRP에서는 Action이 없었기 때문에 agent가 state에 있으면 시스템이 자동적으로 확률에 의해 다음 state로 넘겨줬는데
MDP에서는 Action에 따라 다음 state가 정해져서 Policy가 중요하다. 어떤 정책에 따라 Action을 할것인가.
즉 Policy는 Agent의 Action을 결정해 주는 것.
윗윗 그림에서는 policy가 안나타나져있는데, 저건 environment이고, Policy는 Agent의 영역임.\
그럼 Agent는 내가 어떤 policy를 가지고 Action을 했을때 Return값이 최대로 돌아올까 ? = MDP를 푼다.
- MDP의 Policy는 현재 state에 대해서만 의존한다(history를 볼 필요 없음)
- Policies are stationary (time-independent)


이해하면 좋은 , 그러나 이해 안해도 된다고 하지만 일단 듣자.
MDP에서 내가 어떤 pi(policy)를 가지고 움직인다고 가정해보자. (MDP고정, policy고정)
agent의 policy가 고정이 되면 Markov Process로 생각할 수 있다.
예를들어 state 1번이 있다. state 10번으로 간다고 하자. state로 이동하는 값이 고정이고 policy도 고정이면 그림은 다음과 같다. (지극히 이해한대로 그려본 것이니 부정확할 수 있다.)

그럼 이제 1번에서 어떤 Action을 취해서 10번으로 갈 확률을 Pa1*P12 + Pa2*P12 + Pa3*P12 + Pa4*P12 이다.
이처럼 다 더해주면 Pss^pi를 구할 수 있다.(나중에 티스토리에 수식넣는법을 찾아보자)
이렇게 Policy와 MDP가 고정되면 Markov Process가 된다.
State와 reward sequence도 위와 같이 Markov Reward Process가 될 수있다.

State Value Function
이전 Markov Reward Process에서도 Value Function얘기를 했는데, 그때는 pi가 없었음. 왜냐하면 액션이 없었기 때문에.
이젠 MDP에서 agent가 Policy를 가지게 되었으니 Policy를 가진 agent가 episode(terminate)를 쭉 샘플링 해서 그 값들의 평균값이 MDP의 value function이다.
Action Value Function ( or state action value function )
인풋(given by)이 State만 들어가면 State value Function이고, Action도 함께 들어가면 Action Value Function.
State S 에서 action A를 했을 때 그 이후에는 policy를 따라 끝까지 했을 때. return의 기댓값. Q함수라고 하기도 함.
Q-learning, DQN 이런것들은 이 Action Value Function을 학습시키는 것이다.
이제 했던 얘기들을 Bellman Equation을 이용해서 얘기할것이다.
왜하냐하면 큰문제에서 학습시키는데 벨만 Equation이 기초가 돼서.
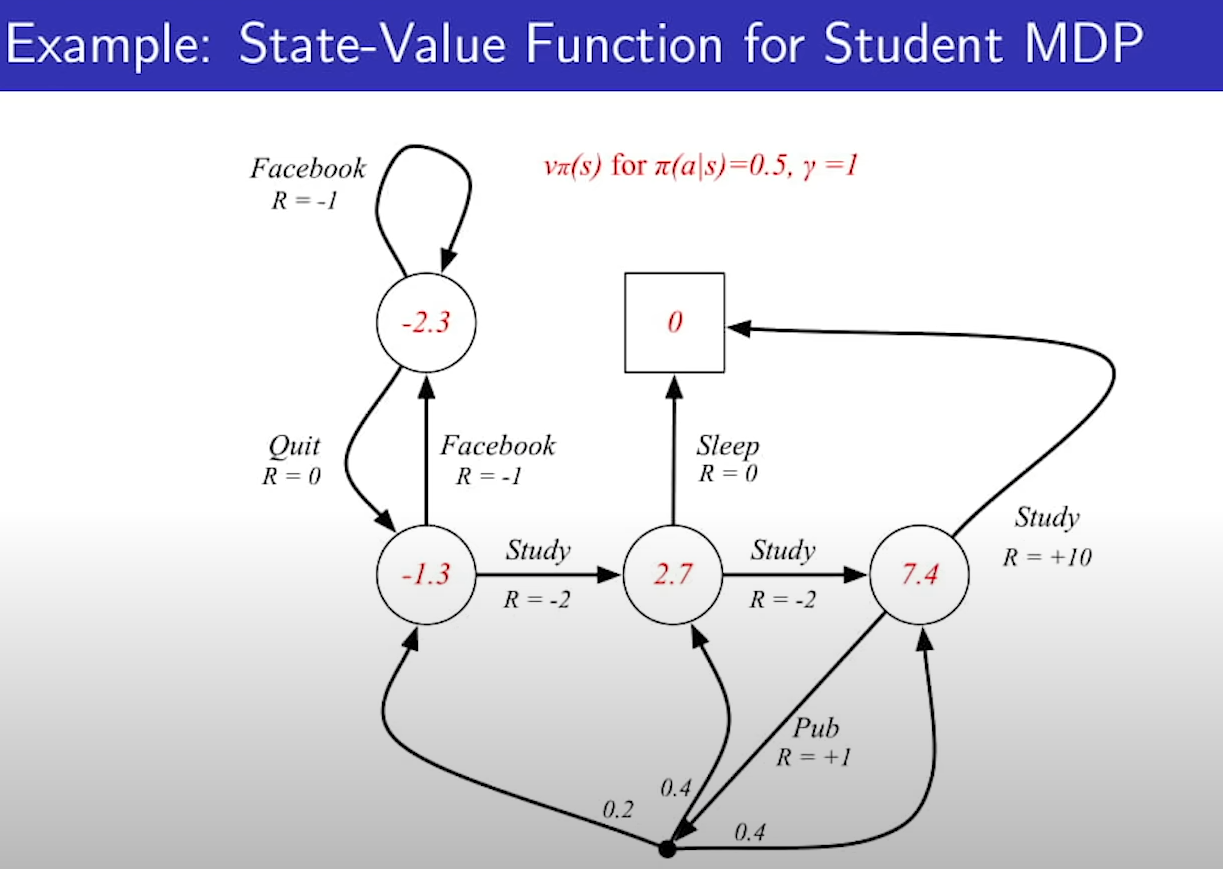
state에서 각 액션을 취할 확률은 0.5라고 가정하고 gamma는 1이다.
Markov Reward Process(이하 MRP)에서는 행렬형태로 나타내고 v를 한쪽에 몰아서 역행렬취하고.. 한번에 계산 했는데.
그 수식도 벨만 Equation으로 부터 나왔고, 이것도 마찬가지.
Bellman Expectation Equation(나중에 Bellman Optimalitic? Equation 그냥 미리 말해봄)

위의 식은 아까 봤던 것인데 pi가 추가된 것이고, Action이 드러나게끔 풀어보면 아래식이 된다.
1번식 해설 : state value function은 일단 1스텝을 가고 그 다음 state부터는 pi(policy)를 따라서 가는것과 똑같다.
2번식 해설 : state s에서 a를 하는 것은 s에서 a를 해서 reward를 하나 받고, 다음 state에서 다음 action(pi에 의해 정해짐)을 하는것의 기댓값과 똑같다.
수식표현 - 행렬표현 - 행렬넘겨서 해 구하는순.

v와 q의 관계
state에서 action할 확률들이 있고. 그 action을 했을 때 action value function이 q인데 그것들의 가중치 합.
마찬가지로 q를 v로 표현할 수 있음.

state에서 action을 할 value라고 함은 일단 Reward를 받고. s에서 a를 하면 어느 state에 떨어질 지 모름.
그래서 어떤 state로 가는 확률과 state s prime에 떨어졌을때의 value function들을 모든 state에 대해서 더해주면 그것이 q이다.
풀어말하면 s에서 a를 했을떄 pi를 따라 끝까지 하면 얻을 return의 기댓값이 q인데. 일단 s에서 a는 하고. 그런데 어떤 state에 떨어질 지 모름. 모든state에 다 갈 수 있음. 그래서 모든 state에 대해서 각 state에 떨어질 확률과 그 state에서의 value를 곱한 것들의 합. // 그런데 그 state에 떨어질 확률은 MDP에서 state transition matrix로 계산한다. 감마는 한스텝 가면 discound해주기 때문에.
v_pi(s)는 감마가 없는데. 한스탭을 간게 아니기때문에 .

v의 q자리에 q를 그대로 대입하면 위의 식이 나옴.
2step을 말로 풀자면, 검은점은 action, 흰점은 state.
s에서의 value는 a를 할 확률이 다 있고. 그 확률 * action value(q) 이다.
그런데 그 action value는 그 state의 reward에다가 gamma*다음state 모든경우의 value의 평균.
이 식을 만든 이유는 행렬로 바꾼다음에 v만 남기고 넘기려고 만들었다.

마찬가지로 q도 q의 v자리에 v를 대입하면 위의 식이 나온다.
이건 사용하진 않을거고 이런게 있다하고 넘어가면 된다.

실제로 위 식들을 써서 만족하는지 보자.
7.4에서 아래부터.
reward 1받고 0.2*-1.3, 0.4*2.7, 0.4*7.4, reward 10 받고 1*0 == 0.5*(1 + 0.2*(-1.3) + 0.4*2.7 + 0.4*7.4) + 0.5*(10+ 1*0)

히이이익 MRP와 똑같은 식.
잘 생각해보면 지금 value function만 구했지 action은 어떻게 해야하는지 구하지 않았음.
MDP의 첫 장이 끝났고 두번째 장 optimal장이 시작 된다. ( 하 힘들다 ;)

optimal부터 정의해보자.
optimal state value function
이번엔 star다. 파이가 아님. 파이는 어떤 policy를 따랐을 때의 value이고. star는 니가 어던 policy를 따르든 무한개의 policy가 있을텐데 그 policy들을 따랐을 때의 value값도 무한개가 있을것임. 그것들 중에 제일 나은 애.
all policies중에서 가능한 maximum값.
optimal action value function.
니가 할 수 있는 모든 policy를 따른 q함수 중에 max값.
optimal value function은 MDP에서 가능한 가장 좋은 성능을 나타낸다.
그래서 이걸 아는 순간 MDP는 풀렸다 라고 한다. (is solved) optimal은 작은 연산에 대해서도 행렬연산으로 풀 수 없다. 왜냐하면 행렬형태로 표현이 안되서.

gamma가 1일 때 optimal value function을 나타냄.
0 - Study3 - Study2-Study 1 순으로 가보면 좀 당연해 보이는 그림이기도 함.
optimal value function에 대해서 배웠으니 optimal policy에 대해서 배워보자.

두 policy가 있다면 어느 policy가 나은지 비교해야 할텐데 이 비교를 partial ordering으로 정의할 것인데
어떤 두 policy가 있다고 해도 항상 두 policy를 비교할 수 있는건 아니다. 대신 어떤 두개에 대해선 비교가 가능하다.라고 전제를 한다. 식을 보면 두 Policy가 있을 때 policy 1이 policy2보다 낫다고 판단하려면
모든 state에 대해서 policy1의 state value function이 policy2의 state value function보다 클때.
너무 한정적인 case같긴한데.. 이를 정의하고 나면 똑똑하신분들이 정리해둔게 있다. 우린 이를 쓸뿐.
There exists an optimal policy pie star that is better than or equal to all other policies,
(MDP에 대해서는 optimal policy가 존재한다 이 policy는 모든 pie에 대해서 partial ordering이 성립된다.)
All optimal policies achieve the optimal value function
(이 policy pie star를 따라가면 그게 곧 v-star와 같다)
Q에 대해서도 똑같이 성립한다.
optimal policy는 하나일 필요는 없고 여러개 일 수 있다.

Q-star를 알면 optimal policy하나는 무조건 찾아진다. 당연한게 Q-star는 s에서 무슨 a를 해야하는지 알려주기 때문에.
중간식 : state에서 Q-star를 알때 Q-star의 action을 할 확률은 1이고 나머지는 다 0인 policy가 있다고 해보자.
그 policy는 Q-star를 따라가는 것 뿐인 policy이다. 걔는 당연히 optimal policy이다.
모든 MDP 문제에서는 determistic optimal policy가 항상 존재한다.
왜냐하면 policy는 본디 stocastic(각 Action에 대한 확률을 알려줌)인데 그런데 하나만 1이고 나머지 다 0이면 deterministic policy가 되어버림.
예를들어 가위바위보가 있다고 해보자. 상대방은 가위바위보를 내는 분포가 있는데, 나는 그에 맞는 determistic policy가 존재한다는 의미임. 상대방이 가위바위보를 내는데, 나는 계속 주먹만 내는데도 그게 optimal하다는 것임. (???)
만약 상대방이 주먹 50% , 보 50%를 낸다고 했을때 나는 보만 내도 50%를 가져갈 수 있음.
그래서 우리가 Q-star를 안다면 Q-star만 따라가면 optimal policy를 얻을 수 있다.

빨간화살표(Q-star)만 따라가면 optimal policy(빨간 선)을 얻을 수 있다.
Optimal policy에 bellman equation을 적용해보자. (bellman optimalitic equation)
(참고로 아까했던건 bellman expectation equation)


아까 했던것과 비슷한 얘기. 리워드 받고 갈 확률과 state의 value곱의 합.

v식에 q를 대입하면 위처럼 된다.
여기서 중요한건 v-star식은 linear equation이 아니다. 왜냐하면 max때문에.
max만 없었으면 넘기고 묶고 역행렬 취하면 되는데 그게 안된다. 이게 optimality과 bellman expectation equation과 다른점

식을 풀어본 예제.

그래서 마지막으로 Bellman Optimality Equation을 푸는것은 non-linear하기 때문에 closed form해가 없다.
그래서 여러 반복적인 솔루션들이 존재하는데, Value Iteration , Policy Iteration, Q-learning, Sarsa가 있다.
value, policy는 dynamic programming.
MP-MRP-MDP순으로 배웠다.
value function , optimal value function ,optimal policy.
그리고 어떻게 푸는지. 간단한거는 해를 구해도 봤고, 해를 못구하면 어떤 방법론이 있는지.
방법론은 차차 뒷강의에서 배워볼 것이다.
'인공지능 > Reinforce_Learning' 카테고리의 다른 글
| [Part 2] Ch1. MDP 실습코드 (0) | 2020.11.18 |
|---|---|
| [Part2] Ch1. 마르코프 결정과정 (0) | 2020.11.18 |
| [Part1] 환경 설정 (0) | 2020.11.18 |
| [Part 1] 강화학습 소개 - 강화학습 대화를 위한 넓고 얕은 수식 (0) | 2020.11.17 |
| [Part 1] 강화학습 소개 - 강화학습이 무엇인가요 어디에 쓸 수 있죠? (0) | 2020.11.17 |