함수 근사란?

파라미터Θ를 조정해서 (x,y)페어를 잘 표현하는 함수를 찾고싶다.
왜 RL강의에서 "함수 근사" 를 배우는가 ?

크게 2가지로 함수근사를 사용하고 배우게 됨.
1. 파트4 정책 최적화에서 정책함수 π를 표현하기 위해서.
2. 파트5 심층강화학습에서 사용하기 위해서
함수근사 사용 효과가 굉장히 좋음.
데이터로부터 함수 근사를 수행할 수 있음.
선형회귀같은 경우에 데이터가 선형이라는 가정을 하고 시작하기 때문에(함수에 대한 구조 가정)
실제 데이터가 선형이 아니라면 정확도가 떨어진다.
그러나 딥러닝같은 경우에는 이런 가정 없이, 충분히 데이터가 많다면 함수를 근사할 수 있다.
데이터를 함축적으로 잘 표현하는 좋은 representation을 배울 수있음 (나중에 배워보자)
좋은 representation이란? 딥러닝에서 데이터의 크기가 크거나, 이미지 같은 것이 주어졌을 때 각각의 픽셀은 의미가 없지만 픽셀들이 모여서 이미지의 의미를 얻어 낼 수 있다. 이것이 기존 강화학습의 성능을 높혀준다.
단점으로는 모든 함수근사가 단점을 가지는 것은 아니고, optimal한 function approximation개념이 존재하는데
optimal하지 않으면 강화학습이 잘 안될거라고 생각했던 때가 있었는데, Deep Q-learning이 생기게 되면서 함수근사 기법이 optimal하지 않아도 잘 작동한다는 것이 실험적으로 증명됨.
가치기반 강화학습 문제의 풀이 기법

강화학습 문제 MDP를 배웠었고, 풀기위한 방법으로 DP, MC/TD를 배웠음.
각각의 상태가치 함수 V, 행동가치함수 Q를 테이블(혹은 tensor)
테이블의 각각의 V,Q값이 독립적으로 추산된다.
그렇다면 실제 V,Q가 독립적일까 ? 그렇지 않음.
V,Q의 값들이 정말 독립적인가 ?

정말 독립적이라면 값에서 패턴을 찾을 수 없었을 것임(-4, -3, -2, -1 ...)
그래서 이런 value function을 close form 함수로 나타낼 수 있음.
만약 Q,V가 Linear하다고 한다면
함수 근사 기법을 활용한 가치함수 추산

초록색 데이터를 알고, Linear할 것이라고 가정을 해둔다면 파란색 데이터도 알 수 있지 않겠는가 ?

선형이라고 가정하면 a,b를 찾을 수 있지 않겠나.
선형회귀 분석

독립변수 x와 종속변수 y를 잘 매칭할 수 있게끔 해주는 w,b를 찾는 것.
L2 norm 관점에서 최적인 파라미터는 ?

예측치 Y hat과 실제값 y간의 거리로 파라미터 최적성을 평가.
Log likelyhood라는 방법도 존재함.
"Addictive losses" + "I.I.D" 가정
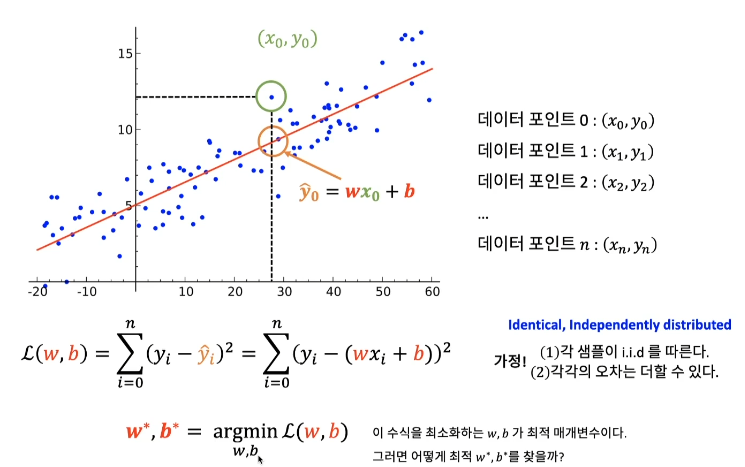
오차함수값을 최소화 시키는 w,b가 존재한다면 w*, b*가 된다.
가정 1. 각각의 샘플이 i.i.d를 따른다.
i.i.d? identical, independently distributed 되었다.
indentical : 모든 값들은 같은 함수에서 샘플이 됐다고 생각함
independently distributed : 샘플링 될때 각각의 값들은 서로 연관이 없다.
그럼 이 파라미터 w*,b*를 어떻게 찾을 수 있을까 ?

아까는 x의 차원이 1이라고 가정했지만 좀더 일반화 하기 위해서 p개의 값으로 구성 되어있다고 생각.
X : 데이터 matrix
최소 자승법을 활용한 선형회귀 모델의 최적 파라미터

이 경우 closed form으로 계산할 수 있다.
항상 가능한건 아님.
X or n, p가 크다면 역행렬 계산이 쉽지 않고.
데이터 매트릭스가 안정도 조건을 가져야 inverse 계산을 할 때 numerically state계산을 할 수 있음.
직접해를 구하는 방법이 존재해도 다른방법을 사용해야 한다.
함수에서 최소값 찾기

극값이 무한히 존재할 수 도있음. 등등... 현실적으로 찾기 힘들 수 있음.
미분과 반복과정으로 답을 찾아보자.

함수값을 minimize하고싶으니, gradient와 반대방향으로 업데이트를 하면 최소값으로 가지 않겠나.
Gradient Descent

미분값에 반대방향으로 업데이트 해가면서 극점을 찾음.

마무리

선형회귀식 : y = wx+b
직접해도 구할 수 있지만 복잡도가 높아질수록 역행렬을 구하기 힘들어지는 계산문제가 있어서 다른 알고리즘을 통해서 구해야한다.
'인공지능 > Reinforce_Learning' 카테고리의 다른 글
| [PART 3] Ch 02. Pytorch로 선형회귀 모델 만들기 (0) | 2020.12.29 |
|---|---|
| [PART 03] CH02. 심층 신경망을 활용한 함수근사(선형근사) (0) | 2020.12.29 |
| [Part2] CH05. Off-policy TD contorl과 Q-Learning (0) | 2020.12.23 |
| [PART2] CH05. Off-policy MC control (0) | 2020.12.23 |
| [PART2] CH04. SARSA TD 기법을 활용한 최적정책 찾기 (0) | 2020.12.22 |